Normalmente cuando se piensa en un programa de cálculo de estructuras, intuitivamente lo asociamos al análisis de esfuerzos en puentes o edificios. En este post vamos sin embargo a explorar una de las posibilidades que ofrece este tipo de software (concretamente SAP2000) más allá de lo que es estrictamente el cálculo de esas grandes construcciones.

En concreto, abordaremos el estudio de algo tan pequeño y bello como es la vibración de la cuerda de una guitarra. Ello nos permitirá servir de base para entender mejor el fenómeno físico, y de paso conocer el modo en que intervienen las diferentes variables que lo controlan.
BREVE DESCRIPCIÓN DEL FENÓMENO FÍSICO
Intuitivamente se entiende que una cuerda elástica en tensión vibra libremente bajo su propio peso tras ser golpeada. Dicha vibración genera un sonido (ondas de choque) cuyo registro se corresponde con el ritmo vibración de la cuerda. Cuanto más tensionada esté la cuerda, mayor será su frecuencia de vibración (el número de veces que oscila por segundo) y por tanto más agudo será el sonido. De la misma forma, a igualdad de tensión, cuanto más reducida sea la longitud de la cuerda, mayor será nuevamente la frecuencia, emitiéndose por tanto un sonido más agudo.

CARACTERÍSTICAS DEL MODELO DE CÁLCULO Y DATOS PRINCIPALES
Para ponerle números a este fenómeno, hemos confeccionado con SAP2000 un modelo analítico de una cuerda de guitarra eléctrica (la cuerda nº1, las más aguda). En principio el modelo parece sencillo, al tratarse de un único elemento recto de sección constante, el cual se encuentra (a efectos prácticos) totalmente empotrado en ambos extremos.

No obstante, hemos de tener en cuenta que dado la frecuencia de vibración parece depender de la fuerza axial de la cuerda (según hemos señalado antes), se trata de un caso donde es especialmente importante tener en cuenta la geometría deformada de la cuerda en el análisis (cálculo con no linealidad geométrica).
Para confeccionar el modelo, hemos recabado de Internet los datos geométricos y mecánicos que necesito, a saber:
– Longitud total libre de la cuerda (distancia entre el puente y la clavijro): Unos 650 mm
– Diámetro de la cuerda: Existen varios diámetros, en función del tipo de cuerda. Un valor habitual para la cuerda nº 1 es de 0.28 mm, tal y como se recoge en la siguiente tabla. El área será por tanto 0.0616 mm2

– Peso especifico y módulo de deformación del material: Al tratarse de cuerdas de acero, se toma un peso específico de 77 kN/m3, y un módulo de deformación de E=200.000 MPa.
– Tensión de trabajo de la cuerda: En internet existen numerosas reglas básicas para determinar la tensión necesaria de una cuerda, en función de sus características mecánicas y la frecuencia requerida. Por ejemplo, incluimos la siguiente extraida del catálogo de cuerdas de la casa D’Addario:

Aplicando la regla anterior, para la cuerda nº1, y según el diámetro considerado, la fuerza total a la que debe estar sometida (la que se introduce durante la afinación) es de unos 86 N Esto hace que la tensión de trabajo de la cuerda sea de casi 1400 MPa. Encontramos por tanto la bonita coincidencia de que la cuerda nº1 de una guitarra trabaja a unos niveles de tensión muy similares a los de los cables de pretensado de los puentes.
Con ello, se confecciona modelo de cálculo, con las características que aparecen a continuación:

La discretización del modelo se realiza automáticamente por el programa en tramos comprendidos entre 5 y 10 mm.
Con este modelo voy a tratar de estudiar los modos principales de vibración de la cuerda bajo su propio peso, teniendo en cuenta la influencia de una fuerza constante de tracción.
OBTENCION DE RESULTADOS DEL MODELO
VIBRACIÓN DE CUERDA AL AIRE Y PRIMER ARMÓNICO
Tras resolver el modelo, se obtiene ya el primer resultado interesante cuya validez se puede contrastar: El primer periodo de vibración de la cuerda es T=0.00306 seg, lo que implica una frecuencia (1/T) de f=327 Hz.


La cuerda que se ha modelizado (cuerda n 1 al aire) debería vibrar a la frecuencia correspondiente a la nota Mi (E) en la octava 3. En la figura siguiente se observa que esa frecuencia es 329.6 Hz (1st string, Open):


Se puede observar por tanto que la frecuencia para la citada nota (Mi_3) es practicamente al valor obtenido en el modelo (327 Hz), con una diferencia de menos de un 1%.
El segundo modo de vibración de la cuerda tiene una frecuencia de 654 Hz (T=0.00153 seg), que corresponde muy aproximadamente con la nota Mi_4. Por la forma del modo de vibración (con amplitud nula en el centro de la cuerda), y por la frecuencia obtenida, se puede ver que se trata del primer armónico que se puede escuchar en cualquier guitarra poniendo el dedo sobre el traste nº12 (situado en la mitad) mientras vibra la cuerda.

DETERMINACIÓN DE LA SEPARACIÓN ENTRE TRASTES
Otro aspecto interesante que se puede estudiar con el modelo realizado, es la forma en que se incrementa la frecuencia de vibración principal de la cuerda (1er modo) conforme se reduce la longitud de la misma. En una guitarra, presionar la cuerda sobre un traste es precisamente la forma de reducir la longitud de vibración de la misma, y por tanto modificar el registro de la nota producida. Conociendo la ley que relaciona la longitud de la cuerda con la frecuencia de vibración, podríamos llegar a conocer las posiciones necesarias de los diferentes trastes en el mástil de una guitarra, teniendo en cuenta la nota que se requiere al pisar cada uno de ellos.
Para obtener la citada ley, he calculado la frecuencia propia de vibración del primer modo, para un rango de longitudes que varían desde los 650 mm hasta los 180 mm, en intervalos de 10 mm. Los resultados obtenidos se resumen en la siguiente tabla:
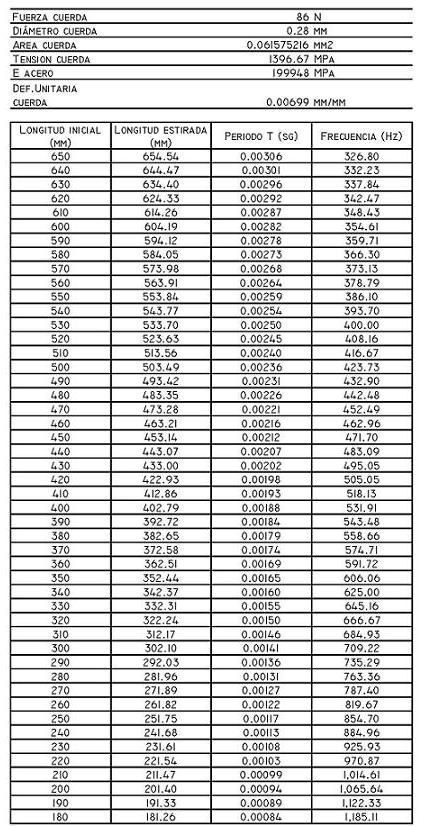
Gráficamente queda de la siguiente forma:

Sabemos que cada traste de la guitarra produce una nota musical medio tono superior a la del traste anterior. Partiendo de la nota Mi_3 (329.64 Hz), podemos introducir en el eje de ordenadas, y a modo de líneas horizontales, la frecuencia de las 22 notas siguientes, hasta llegar a la nota Re_5 (1174.72 Hz), que es normalmente la mas aguda que se puede producir con los trastes de una guitarra eléctrica clásica (una Strato por ejemplo). La intersección de esas líneas horizontales con la curva obtenida anteriormente, nos tendría que dar las distancias a la que deben situarse los diferentes trastes en el mástil de una guitarra.
En el siguiente gráfico se observan las distancias de los trastes obtenidas según lo indicado en el párrafo anterior. Para comprobar la validez de los resultados, se ha introducido la foto (escalada al gráfico) del mástil de una Fender Stratocaster:

CONCLUSIÓN
En este post hemos puesto un ejemplo de la ámplia variedad de fenómenos físicos que pueden ser analizados con un programa de cálculo de estructuras. El de hoy nos ha permitido conocer un poco mejor algo tan bonito como es la vibración de las cuerdas de una guitarra, situar en orden de magnitud las diferentes variables que intervienen en el proceso, así como conocer la relación entre ellas.
Muchas gracias por vuestro interés.
Páginas web consultadas para la elaboración del presente post:
- (1) http://www.frudua.com/tension_cuerdas_guitarra.htm
- (2) https://www.guitar.com/articles/completetechnical-reference-fretted-instrument-string-tensions
- (3) http://www.uq.edu.au/_School_Science_Lessons/UNPh26.html
¿Quieres ser el primero en leer nuestros artículos?
Déjanos tu nombre y un email válido, y nosotros te avisaremos cuando hayan novedades en Estructurando
 |








¡Qué interesante y original!
Si ya era Estructurando.net una página con grandes posts, colaboradores así la van a hacer aún mejor.
Feliz 2016!
Felicitaciones, un excelente análisis.
Será posible comentar una solución para cubrir grandes luces industriales de un piso con columna separadas, por ejemplo cada 729 m2 y techo inclinado plano máximo 10° o columnas separadas cada 1,800 m2 con techos curvos.
Muchas gracias
Alberto
Muy original!! Me ha encantado felicidades al autor!
Qué análisis más curioso y más bonito! Enhorabuena al autor y a Estructurando 🙂
Así pues, SAP hace análisis no lineal teniendo en cuenta No linealidad geométrica…¿se podría entonces entender la cuerda como un tirante sometido a su peso propio y con una tensión de tesado? Muy interesante!
Gracias por los comentarios. Respondiendo a Isabel, efectivamente se puede encontrar una gran similitud entre el tirante de un puente y un cuerda de guitarra. De hecho un procedimiento habitual para determinar la fuerza real a la que está sometido un tirante (conociendo su sección, longitud y peso por metro lineal) es medir mediante una excitación exterior, la frecuencia de vibración del mismo.
Felicitaciones por explicar el maravilloso enlace de los números con la música. Un Ingeniero integral.
Me ha parecido muy interesante. De hecho, me gustaría reproducir los cálculos pero no sé cómo considerar la tensión de la cuerda en el cálculo modal. ¿Me podrías orientar? Muchas gracias. Un saludo