Un caso especial que se suele dar con frecuencia en depósitos o torres es que su zapata sea de forma anular con simetría de revolución.

En este caso, el cálculo de esfuerzos para armar la zapata no es inmediato y no suele venir recogido en los programas de cálculo convencionales.
En este post os dejamos una metodología para poder obtener los esfuerzos de una zapata anular y así poder armarla convenientemente.
El primer paso es calcular las propiedades geométricas de la cimentación.
Supongamos que tenemos una zapata anular de radio exterior r2 y de radio interior r1, entonces el área y momento de inercia de la cimentación vendrá dada por:
Y el radio al centro de gravedad de la zapata, r0, viene dado por:

Y si la zapata tiene un canto C, el momento de inercia a flexión y a torsión de la zapata vendrá dado por:

El segundo paso es obtener el giro de la zapata debido al Momento que la solicita, con la expresión:


Donde:
E es el módulo de deformación del hormigón
G es el módulo de elasticidad transversal que podemos tomar:

ν es el módulo de Poisson del hormigón (por lo general 0.2)
Kc es el módulo de balasto de la zapata (por si no sabes cómo calcularlo, lo explicamos en un post hace poco titulado “Breve resumen del coeficiente de balasto”.
El tercer paso, es comprobar las tensiones bajo la zapata y para eso solo tenemos que usar la ley de Navier:

Ojo con que no se despegue la zapata ni superemos las tensiones admisibles.
Por último, obtener los esfuerzos para los cuales hay que armar la zapata. Basta con seguir las siguientes fórmulas:
- Momento para armar a flexión perimetral:

- Momento para armar a torsor:

- Momento para armar a flexión transversal:
El mayor valor de los dos momentos siguientes:

Donde las tensiones son:


- Cortante para armar o comprobar la zapata:

Espero que os pueda ser útil e interesante.
Fuente: JALIL, W.A.: “Calcul des Fondations Annulaires et Circulaires d’ouvrages de Révolution” Annales de l’Institu Technique du Bâtiment et des Travaux Publics, Junio 1969
¿Quieres ser el primero en leer nuestros artículos?
Déjanos tu nombre y un email válido, y nosotros te avisaremos cuando hayan novedades en Estructurando
 |



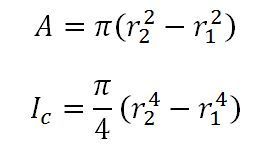





Gracias por la enseñanza
Gracias a ti por leernos.
Saludos.
Muy agradecido.
Saludos, he estado estudiando tu artículo y no me es claro dos cosas en el cálculo de J, ellas son:
Que es b?
La sumatoria como se explica?
Hola Ricardo,
b es realmente C, se me olvidó cambiar la letra cuando ajusté la fórmula. En cuanto tenga un hueco cambio la formula y paso b a C. Y en cuanto a la sumatoria, se trata de una sumatoria de los términos impares naturales de 1 a infinito. Esta fórmula no es mas que la fórmula de inercia a torsión de un rectángulo de base (r2-r1) y de altura C.(Cuando ajusté la fórmula a los parámetros del problema del post es cuando se me pasó el cambio de b por C).
Espero haber resuelto tus dudas. Un saludo.
Buenas… disculpa mi ignorancia… que serías los términos v1 y v2? distancias del borde de la zapata a la cara de la columna?
muchas gracias!
Hola Roberto,
Aunque te han contestado ya, te confirmo que v1 y v2 son los vuelos de la zapata, es decir, la distancia del borde de la zapata a la columna. Se me olvidó ponerlo en el esquema de la zapata. Voy a cambiar en el esquema para que aparezca.
Un saludo.
Otra consulta… (no quiero ser molesto) Para determinar el coeficiente de balasto vertical, suponemos una sección cuadrada de ancho r2-r1 y largo igual? Como corregimos el k30 para este caso? (no encontré en la web conversiones de k30 para zapatas circulares ni anulares) Muchas gracias
Hola Roberto,
Me voy a tomar el atrevimiento de responder tus preguntas (ya que me estudié el artículo) v1 y v2 efectivamente son las distancias que indicas; por otro lado en un proyecto en el cual llegase a requerirse una cimentación de ese tipo es casi seguro que hay un estudio de suelos de donde puedas obtener la respuesta; si no es así, yo me acomodaría con la ecuación de Bowles que está solamente relacionada a la capacidad del suelo.
Gracias por responder. Acertastes. Ya he puesto las cotas de v1 y v2 en el dibujo para que se vea mas claro.
Un saludo.
Muchas gracias!
Hola Roberto,
Pregunta todo lo que quieras. No es molestia.
Buena pregunta la que planteas. En bibliografía especializada he visto que cogen la K de la zapata rectangular de ancho (r2-r1). Creo que en arenas podría valer pero si el suelo es arcilloso quizás es una burda simplificación y en ese caso habría que corregir por L y tomaría esta la longitud total del anillo de radio r0. Supongo que la verdadera K estará entre esos dos valores por lo que sería interesante coger las dos y ver que pasa con los esfuerzos (estudio de sensibilidad) y coger los mas desfavorables.
Un saludo.
Muchas gracias…
Me he topado con este excelente blog cuando buscaba información sobre el módulo o coeficiente de balasto.
Hay que felicitar a los autores, pues es muy escaso el material de calidad sobre los temas que aquí se publican. Posts cortos, concisos y muy claros. Al mejor estilo técnico de altura. Por favor, sigan adelante con este proyecto!
—
En relación con este artículo, quizás sea pertinente acotar que para el caso de los muros que, normalmente acompañan estas zapatas anulares, es mejor “ver” el problema en planta: los muros tienen un comportamiento más parecido a ductos bajo presión, y su refuerzo circunferencial (o tangencial, como gusten llamarlo) suele ser mayor que el vertical.
Esto ocurre, por ejemplo, en el caso de muros de silos, cuya carga o presión radial es mucho mayor que la vertical (por cierto, las cargas en los silos se pueden obtener con una excelente aplicación gratuita del Dr. Dietmar Schulze, en http://www.dietmar-schulze.de/).
Ese comportamiento se entiende mejor si se ve la estructura en planta en lugar de ver su elevación o sección vertical.
Es también el caso del aliviadero (vertedero) de la presa Guri, el cual se diseñó en forma de cuña (visto en planta los monolitos son sectores de círculo), o de los anillos de distribución y de descarga de una turbina Kaplan (ductos verticales a presión).
Sobre esto escribí un artículo que está en: http://civilisstructurae.blogspot.com/2015/06/comportamiento-de-los-muros-circulares_10.html
Saludos y gracias por haber realizado este excelente blog!
En el cálculo del momento a torsión J que es k, gracias
Buenas
Aprovechando el tema de cálculo de cimentaciones quisiera consultar si alguien tiene referencia del cálculo de losas de cimentación circulares, por ejemplo para tanques de agua, ya que no tengo claro cómo calcular el acero a flexión si se usa una parilla ortogonal a diferencia de un losa rectangular dónde se analizan 2 direcciones principales y el refuerzo se coloca paralelo al plano de análisis
Gracias
Buenas
Aprovechando el tema quisiera saber si alguien tiene referencia sobre la metodología de cálculo para losas de cimentación circulares, por ejemplo para un tanque de agua, ya que no tengo claro el cálculo del acero a flexión si se utiliza una parrilla de acero ortogonal por en lugar de refuerzo radial y circunferencial que da igual capacidad en todas direcciones pero podría ser más difícil desde el punto de vista constructivo. En una losa rectangular, hay 2 direcciones principales y para análisis a flexión y colocación del acero en esas direcciones pero en una losa circular no lo tengo claro
gracias.
buenas tardes
es posible imprimir el post?
gracias
Buenas muy buena el artículo una pregunta también se puede aplicar con columnas directamente en la fundación anular
Estimados de Estructurando:
Se me ha presentado un caso de cálculo de una platea circular de 18 m de diámetro sobre la que va a apoyarse un depósito de líquidos con una altura de 8m. Para peor, la misma se va a construir sobre relleno con aporte de suelo seleccionado y compactado según especificaciones del mecánico de suelos, lo cual me hace pensar seriamente en los procesos de asentamiento y consolidación. Quisiera si me pueden orientar con bibliografía específica sobre cómo tratar el tema. Soy usuario de Cype y habiendo hecho la prueba, obviamente da esfuerzos nulos por tratarse de carga uniforme y coeficiente de balasto uniforme.
Gracias desde ya y saludos a todos.
temas de mucho interes y precision en la informacion. gracias por estas aportaciones. Jaime desde Puebla, Mexico